Hello, I’m new to DGL, but your efforts look great!
I’m interested in using your TreeLSTM code on dependency parse trees (i.e., the child-sum variant of TreeLSTMs). After training on the trees, I’d merely like to get the hidden layer representations from various (or all) nodes in the tree. What’s the easiest way to do this? (I’m new to PyTorch, so I apologize).
Thanks!
Thank you for the kind words.
In dgl, to fetch the node features for some nodes, see the example below:
import dgl
import torch
g = dgl.DGLGraph()
g.add_nodes(4)
g.ndata['h'] = torch.tensor([[0.], [1.], [2.], [3.]])
# To fetch the feature h of all nodes
g.ndata['h']
# To fetch the feature h of a subset of nodes 0, 2, 3
g.nodes[0, 2, 3].data['h']
If you want to preserve some intermediary representations, you can simply store them in the data frames and make sure that they are not overwritten. Taking the TreeLSTM tutorial as an example, the TreeLSTMCell is given below:
class TreeLSTMCell(nn.Module):
def __init__(self, x_size, h_size):
super(TreeLSTMCell, self).__init__()
self.W_iou = nn.Linear(x_size, 3 * h_size, bias=False)
self.U_iou = nn.Linear(2 * h_size, 3 * h_size, bias=False)
self.b_iou = nn.Parameter(th.zeros(1, 3 * h_size))
self.U_f = nn.Linear(2 * h_size, 2 * h_size)
def message_func(self, edges):
return {'h': edges.src['h'], 'c': edges.src['c']}
def reduce_func(self, nodes):
# concatenate h_jl for equation (1), (2), (3), (4)
h_cat = nodes.mailbox['h'].view(nodes.mailbox['h'].size(0), -1)
# equation (2)
f = th.sigmoid(self.U_f(h_cat)).view(*nodes.mailbox['h'].size())
# second term of equation (5)
c = th.sum(f * nodes.mailbox['c'], 1)
return {'iou': self.U_iou(h_cat), 'c': c}
def apply_node_func(self, nodes):
# equation (1), (3), (4)
iou = nodes.data['iou'] + self.b_iou
i, o, u = th.chunk(iou, 3, 1)
i, o, u = th.sigmoid(i), th.sigmoid(o), th.tanh(u)
# equation (5)
c = i * u + nodes.data['c']
# equation (6)
h = o * th.tanh(c)
return {'h' : h, 'c' : c}
Both reduce_func and apply_node_func return a dictionary. The dictionary maps the name of node features to their values and the returned dictionary will be merged into g.ndata. In this implementation, we are overwriting the node feature h. If you do not want to overwrite it, simply give a different name in the returned dictionary, say h0.
Thanks so much for the very fast response. I’ve spent today trying to alter it for my purposes but still have several fundamental questions. I’m hoping to use DGL for a conference paper and my PhD dissertation 
Q1: within the dgl/examples/pytorch/tree_lstm/train.py example, it seems the hidden layers are updated within the nested for-loops of that iterate through each epoch and then step,batches. Since I want to extract the hidden representations of a learn tree, it’s these h’s that I should save to a dictionary, right? Even if this is correct, how do we know the ordering of the h’s? For example, using the “tiny” training set of 5 trees, we have 273 nodes (and thus 273 hidden layers), but how do we know which of these 273 correspond to which element in the original 5 trees?
Q2: Your examples (which are great, btw) are for sentiment analysis, whereby we have a label for every single node in the tree. My first goal is for a completely unsupervised tree (dependency parsed trees) to just learn embeddings naturally, just like how a traditional LSTM is unsupervised, without labels. Which files should I be editing and what’s the easiest way to make these changes? Additionally, my ultimate goal is to do something similar to the sentence classification goal, but instead of the supervision being done by comparing the root of two trees, a few nodes within a given tree should (or should not) have the same label as other sporadic nodes within another tree. Do you envision these being easy changes within DGL or should I try to write it from scratch using PyTorch?
Thanks!
Q1:
The h's are node features in trees. The tree representations can be obtained by some function taking into node features, edge features, tree structure, etc. Since you are interested in the learned representations, you will only need to save the results for the last epoch.
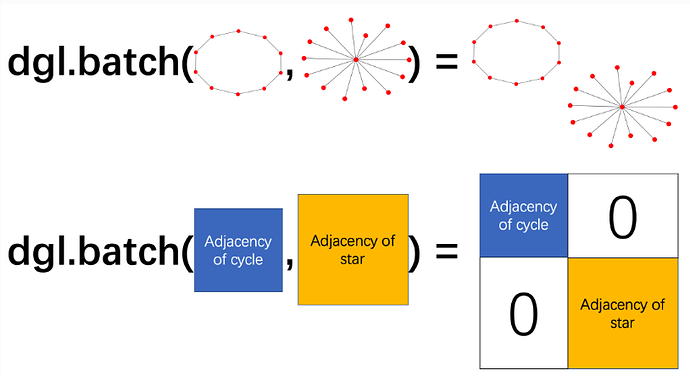
In dgl, when we batch a collection of graphs/trees, we are essentially merging them into a giant graph with several isolated connected components:
Then in the example you gave this means we will have a graph consisting of 5 isolated connected components, with a total number of 273 nodes. The nodes in the new giant graph are re-indexed as consecutive integers starting from 0. The example below might be helpful:
import dgl
import torch
g_list = []
# Create a list of graphs respectively having 1, 2, 3 nodes
for i in range(3):
g = dgl.DGLGraph()
g.add_nodes(i + 1)
# The node features for the 3 graphs are separately
# [[0]], [[1], [2]], [[3], [4], [5]]
start = sum(range(i + 1))
g.ndata['h'] = torch.range(start, start + i).view(-1, 1)
g_list.append(g)
# Merge the list of graphs into one giant graph
bg = dgl.batch(g_list)
print(bg.ndata['h']) # [[0], [1], [2], [3], [4], [5]]
# You can also query the number of nodes in each original graph
print(bg.batch_num_nodes) # [1, 2, 3]
With the batched graph, the node features in all original trees can be updated in parallel. Note that the update happening in batched graph will not come into effect on the original graphs. You can convert the merged large graph back into the small graphs and replace the original g_list.
bg.ndata['h'] += 1
print(bg.ndata['h']) # [[1.], [2.], [3.], [4.], [5.], [6.]]
print(g_list[2].ndata['h'] # [[3.], [4.], [5.]]
# Replace the original list of graphs
g_list = dgl.unbatch(bg)
for i in range(3):
print(g_list[i].ndata['h']) # [[1.]], [[2.], [3.]], [[4.], [5.], [6.]]
Q2:
You can always store different node features and use these node features to compute some objective function. If you want to use some your own dataset, you can write a dataset class yourself. The source code for SST is here for your reference.
For the last part,
Additionally, my ultimate goal is to do something similar to the sentence classification goal, but instead of the supervision being done by comparing the root of two trees, a few nodes within a given tree should (or should not) have the same label as other sporadic nodes within another tree.
my very rough feeling is that you want to compute the pairwise (dis-)similarity between node embeddings from different trees. My feeling is that it might be more straightforward to write some PyTorch code yourself.
Your answers are not only incredibly helpful but also possibly the best customer-service I’ve ever witnessed, haha. Thanks so much for the quick response. I’ll carefully try this out and decide if long-term I should either stick w/ DGL or do it with PyTorch natively.