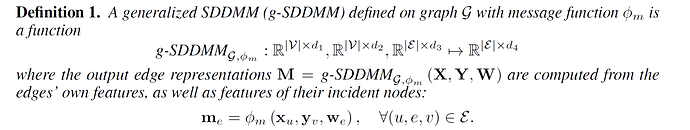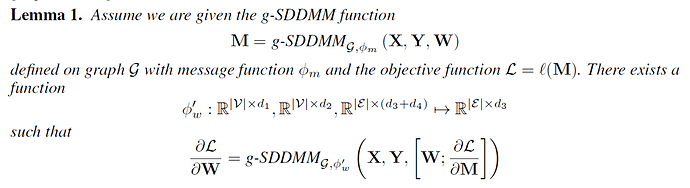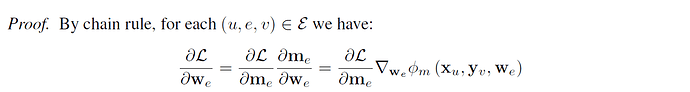I’m very confused about the gradient formulation of gsdmm and gspmm.Take sddmm as example, here is the definition of sddmm, X, Y, W are src node feat, dst node feat and edge feat:
First, the gradient \frac{\partial L}{\partial W } is a gsddmm, the Proof is a little brief and difficult to me to understand, Why this proof can prove Lemma 1 by giving gradient \frac{\partial L}{\partial w_e } . And why the \phi ' _w is \phi ' _w: R^{|V| * d_1}, R^{|V| * d_2}, R^{ |\varepsilon| * (d_3 + d4)} \mapsto R ^ {|\varepsilon| * d_4} while \phi _w is \phi _w: R^{|V| * d_1}, R^{|V| * d_2}, R^{ |\varepsilon| * (d_3)} \mapsto R ^ {|\varepsilon| * d_4} , why the third dim of \phi ' _w is (d_3 + d_4)
I would appreciate it if someone could give me a little advice.