How to implement relational softmax?

[lipingcoding]

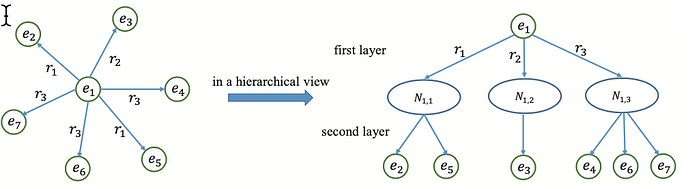
Similar to this this question. I’d like to implement relational attention proposed in this paper

Hi, I’d like to implement the function as follows:


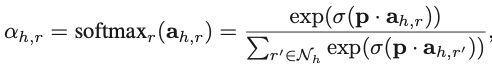
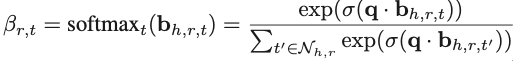
That is, I need to calculate the attention alpha between the head entity and relations, and need to calculate the attention belta between relation and tail entity.
So, How can I use dgl to implement attention score in terms of a part of neighbors, not all neighbors?
Note: I can implement it in the numerator, but it’s not clear how do I compute the denominator


The above is the explanation of the Dimension of the tensor in the softmax function where num_edge is the number of all edge_index.

I find it difficult to compute alpha and beta at the same time. If I filter index via edge_type, that is I focus on the subgraph about relation_i. Then beta attention could be implemented while alpha is still hard to address.
For example, if I mask edge_type i, then in the self.propagate, the edge_index is all about r_i. So as for attention alpha, I couldn’t know the other relations which are the neighbors about entity u.

The desired final result shows below:
For example:
attention_{e_1,e_2} = alpha_{e_1,r_1} * beta_{r_1,e_2}

Looking forward to your help! Thanks a lot!

[mufeili]

The code snippet below works for a single relation.

import dgl
import dgl.function as fn
import torch
import torch.nn as nn
from dgl.nn.functional import edge_softmax

num_nodes = 10
num_edges = 50
emb_size = 5
g = dgl.rand_graph(num_nodes, num_edges)
rg = dgl.reverse(g)
# Initialize entity embeddings
ent_embed = nn.Embedding(num_nodes, emb_size)
h = t = ent_embed.weight
# relation embedding
rel_embed = nn.Embedding(1, emb_size)
v_r = rel_embed.weight
W1_left = nn.Linear(emb_size, emb_size, bias=False)
W1_right = nn.Linear(emb_size, emb_size, bias=False)
# broadcasting
a_h_r = W1_left(h) + W1_right(v_r)
p_embed = nn.Parameter(torch.randn(emb_size, 1))
g.ndata['alpha_h_r_logits'] = torch.sigmoid(torch.matmul(a_h_r, p_embed))
g.apply_edges(fn.copy_u('alpha_h_r_logits', 'alpha_h_r_logits'))
alpha_h_r = edge_softmax(g, g.edata.pop('alpha_h_r_logits'))

# Time for beta
W2_left =  nn.Linear(emb_size, emb_size, bias=False)
W2_right = nn.Linear(emb_size, emb_size, bias=False)
g.ndata['b_h_r_t_left'] = W2_left(a_h_r)
g.ndata['b_h_r_t_right'] = W2_right(t)
g.apply_edges(fn.u_add_v('b_h_r_t_left', 'b_h_r_t_right', 'b_h_r_t'))
q_embed = nn.Parameter(torch.randn(emb_size, 1))
beta_r_t_logits = torch.sigmoid(torch.matmul(g.edata['b_h_r_t'], q_embed))
# There is an one-on-one correspondence between the edges in 
# the original graph and the edges in the reverse graph
beta_r_t = edge_softmax(rg, beta_r_t_logits)
mu_h_r_t = alpha_h_r * beta_r_t