DGMG Decision Sequence

Questions
#1

I am trying to represent a set of temporal edges in a decision sequence to work with DGMG. It’s not clear the correct format when looking at both cycles and molecule example.

As an example, here is a sample set of temporal edges; First two columns define the edge, and the last column define the timestamp.
0,1,10
1,2,20
0,2,30
…

I am looking to develop a code that would be generic across any set of temporal edges. Moreover, the nodes and edges could have types similar to molecule example.

#2

Hi,

The generation of graphs with DGMG follows the finite state machine below

With the molecule example, I preprocess the graphs to get decision sequences for recovering them with the DGMG generation semantics. In particular, they are represented as a list of 2-tuples. The t-th element of the list represents the t-th action to be taken with a 2-tuple. See the sequence extraction code.

#3

Hello,
Thanks for the quick response.
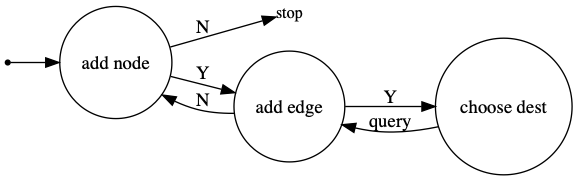
I noticed above code segment. However, I want to understand the general pattern of producing such sequence for a set of temporal edges. You can correct me in the following example:
Edge list have the temporal edges in the chronological order, where first two columns represent the nodes, third column represents the edge type, and the last column is the timestamp.

edge_list = [[0,1,"Type_A",10],
[1,2,"Type_A",20],
[0,2,"Type_B",30]]

add_set=set()
decision_sequence=[]
for edge in edge_list:
        id1=edge[0]
        id2=edge[1]
        edge_type=edge[2]

        if id1 not in add_set:
            decision_sequence.append((0,node_type_to_id[id1])) ## Add Node
            add_set.add(id1)
            
        if id2 not in add_set:
            decision_sequence.append((0,node_type_to_id[id2])) ## Add Node
            add_set.add(id2)
            
       decision_sequence.append((1,edge_type_to_id[edge_type])) ## Add Edge Type
       decision_sequence.append((2,id2)) ## Add destination
        
       decision_sequence.append((1,no_of_edge_types)) ## Stop Adding Edge
decision_sequence.append((0,no_of_node_types)) ## Stop Adding Nodes

node_type_to_id and edge_type_to_id are dictionaries that map given node or edge to an arbitrary type.

#4

There are still some differences between what we are doing. My decision generation code proceeds as follows:

  1. Add node 0. Stop adding edges.
  2. Add node 1. If node1 is connected to node0, add an edge. Stop adding edges.
  3. Add node 2. If there are edges between node 2 to node 0 or node 1, add them. Stop adding edges.
  4. …
  5. Stop adding nodes.

Therefore the termination of adding edges only occurs if there are no edges to add between the latest node and the existing nodes. Meanwhile, you enforce the termination of adding edges every time an edge is added.

1 Like