DGL claims "There are 0-in-degree nodes in the graph" when there are none

[gudeh]

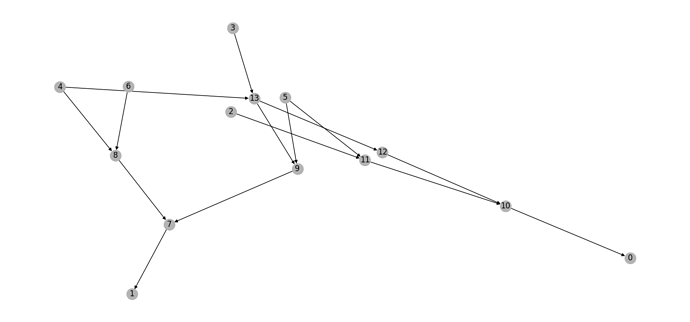
Hi there. I used a piece of code from other post on the forum to remove isolated nodes. You can see a printscreen of a small graph after isolated nodes have been removed. It seems to not have any 0-in-degree nodes as DGL claims.

When I try to perform training with this graph DGL outputs:

File “/home/gudeh/.local/lib/python3.10/site-packages/dgl/nn/pytorch/conv/gatconv.py”, line 254, in forward
raise DGLError('There are 0-in-degree nodes in the graph, ’
dgl._ffi.base.DGLError: There are 0-in-degree nodes in the graph, output for those nodes will be invalid. This is harmful for some applications, causing silent performance regression. Adding self-loop on the input graph by calling g = dgl.add_self_loop(g) will resolve the issue. Setting allow_zero_in_degree to be True when constructing this module will suppress the check and let the code run.

I am using the same model definition as the PPI example (class GAT), although I have to add “allow_zero_in_degree=True” for the code to work.

From the documentation on GATconv it should be bad for training to have 0-in-degree nodes, so I would like to not have them, if possible. What can I do?

class GAT( nn.Module ):
	def __init__( self, in_size, hid_size, out_size, heads ):
		super().__init__()
		self.gat_layers = nn.ModuleList()
		print("\n\nINIT GAT!!")
		print("in_size:", in_size)
		print("hid_size:", hid_size)
		for k,head in enumerate( heads ):
			print("head:", k,head)
		print("out_size", out_size)
		self.gat_layers.append( dglnn.GATConv( in_size, hid_size, heads[0], activation=F.elu, allow_zero_in_degree=True ) )
		self.gat_layers.append( dglnn.GATConv( hid_size*heads[0], hid_size, heads[1], residual=True, activation=F.elu, allow_zero_in_degree=True ) )
		self.gat_layers.append( dglnn.GATConv( hid_size*heads[1], out_size, heads[2], residual=True, activation=None, allow_zero_in_degree=True ) )

	def forward( self, g, inputs ):
		h = inputs
		for i, layer in enumerate( self.gat_layers ):
			h = layer( g, h )
			if i == 2:  # last layer 
				h = h.mean(1)
			else:       # other layer(s)
				h = h.flatten(1)
		return h

[minjie]

Hi, there are indeed zero in-degree nodes in the graph, e.g., node 4, 6, 3. Although they do have out-edges, they won’t receive any messages from in-neighbors.

[gudeh]

Alright! I was confusing 0-in-degree with isolated nodes (when a node has both 0-in and 0-out degrees).

Either way, I would like to know if it is ok for training to happen properly on DGL with a graph such as this. I will always have nodes with 0-in-degree OR 0-out-degree on the graphs that I have. Since I am working with logic circuits, and the circuit inputs will never have any in-degrees and circuit outputs will never have any out-degrees.

That being said, I have some open questions:

1. Do I have to add self loops because of 0-in-degrees and 0-out-degrees noeds? It seems to be the case from this forum discussion.

2. Is adding self loops the same as setting “allow_zero_in_degree=True” in the model definition?

3. Is it possible that including self loops may compromise learning?

4. Is it possible that “allow_zero_in_degree=True” may compromise learning?

[minjie]

@gudeh

Do I have to add self loops because of 0-in-degrees and 0-out-degrees noeds? It seems to be the case from this forum discussion.

There are two common practices: adding self loops and adding reverse edges. In many cases, it is beneficial to collect information from out-neighbors (e.g., in your example, node 3 will then know it has an out-neighbor node 13 which connects to many other nodes). To keep edge directions, you could try assigning them with different initial features or mark the original edges and the added reverse edges with different relations, which turns to a heterogeneous graph.

@gudeh

Is adding self loops the same as setting “allow_zero_in_degree=True” in the model definition?

No. allow_zero_in_degree simply suppresses the error and lets the module run. The actual outcome depends on the model formulation. For example, in GCN, the embeddings of zero degree nodes will become zero after message passing; while in GraphSAGE, only the neighbor embeddings will become zero while the model explicitly carry over the self embeddings.

@gudeh

Is it possible that including self loops may compromise learning?

I haven’t encountered any. Adding self loops is like fixing a corner case which is mainly to avoid erroneous calculation.

@gudeh

Is it possible that “allow_zero_in_degree=True” may compromise learning?

This is possible and that’s why we implemented this check. One example is in GCN, the embeddings of zero degree nodes will become zero after message passing, making them indistinguishable.

[gudeh]

Thanks a lot for the clarifications @minjie!!

Do you think it is a good idea to include the self loops than? Is it safe, considering it seems to add self loops to all nodes in the graph, or can I include self loops on only the 0-in-degree nodes to cover only the corner cases?

By the way here is an image of the training I am getting so far. Each X (horizontal) value is a combination of cross-validation from 10 graphs. And Y (vertical) values are kendall rank correlation achieved for trainig, valid and test (always 1 graph for validation and 1 graph for test). Each one is a run with 110 epochs. The GNN is learning something, although I hope to raise this values after successfully removing the “allow_zero_in_degree=True” option.

[minjie]

Another explanation for why adding self loops for all the nodes is usually fine. Let the adjacency matrix of the graph be A. Then adding self loops is essentially \hat{A}=A+I. One can easily show that A and \hat{A} have the same set of eigen vectors. In general, if your graph is sufficiently large, the added self loops have very little impact.

Good luck with your experiments!

[gudeh]

I see!

These are the graph sizes I have for Vertices (V) and Edges (E). Do you think it is a good idea to remove small ones?

train size: 8

>>> 0  -  jpeg_encoder 		V: 55152 E: 88974
>>> 1  -  swerv 		    V: 75766 E: 137098
>>> 2  -  ibex_core 		V: 14796 E: 25840
>>> 3  -  gcd 		        V: 350 E: 564
>>> 4  -  dynamic_node 		V: 9744 E: 14722
>>> 5  -  ariane 		    V: 2521 E: 3912
>>> 6  -  bp_be_top 		V: 1576 E: 2238
>>> 7  -  RocketTile 		V: 21763 E: 36085

Total Vertices: 181668
Total Edges: 309433

valid size: 1

>>> 0  -  black_parrot 		V: 777 E: 1486

Total Vertices: 777
Total Edges: 1486

test size: 1

>>> 0  -  aes_cipher_top 		V: 12751 E: 20708

Total Vertices: 12751
Total Edges: 20708

[minjie]

I think they are fine.

[gudeh]

Unfortunately by adding the self loops the results got worst!!

I added the self loops at the end of this code:

def _process_single( self, designPath ):
        nodes_data = pd.read_csv( designPath / 'preProcessedGatesToHeat.csv', index_col = 'id' )
        nodes_data = nodes_data.sort_index()
        edges_data = pd.read_csv( designPath / 'DGLedges.csv')
        edges_src  = torch.from_numpy( edges_data['Src'].to_numpy() )
        edges_dst  = torch.from_numpy( edges_data['Dst'].to_numpy() )

        df = nodes_data[ listFeats + [ labelName ] ]
        df_wanted = np.logical_and ( np.where( df[ rawFeatName ] > 0, True, False ), np.where( df[ labelName ] >= 0, True, False ) )
        df_wanted = np.invert( df_wanted )
        removedNodesMask = torch.tensor( df_wanted )
        idsToRemove = torch.tensor( nodes_data.index )[ removedNodesMask ]
        
        self.graph = dgl.graph( ( edges_src, edges_dst ), num_nodes = nodes_data.shape[0] )
        self.graph.ndata[ featName ] =  torch.tensor( nodes_data[ listFeats ].values )
        self.graph.ndata[ labelName  ]  = ( torch.from_numpy ( nodes_data[ labelName   ].to_numpy() ) )

        self.graph.remove_nodes( idsToRemove )
        isolated_nodes = ( ( self.graph.in_degrees() == 0 ) & ( self.graph.out_degrees() == 0 ) ).nonzero().squeeze(1)
        self.graph.remove_nodes( isolated_nodes )
        self.graph = dgl.add_self_loop( self.graph ) 

        return self.graph

This is before adding the self loops:

And this is after adding the self loops:

Average kendall test values went from 0.08 to 0.05 !

[minjie]

Sorry to see that happens ! Is your case a graph classification task or a node classification task? Also, have you tried adding reverse edges?

[gudeh]

Nevermind! I discovered other issues unrelated to 0-in-degree nodes. I will fix them and make sure the self loops were beneficial.